# 线性回归的代价函数
INFO
代价函数是关于的函数
表示第个样本
# 梯度下降
通过梯度下降,找到的局部最优解
INFO
学习率
注意所有的是同时更新的
# Logistic 回归

# Logistic 回归的代价函数
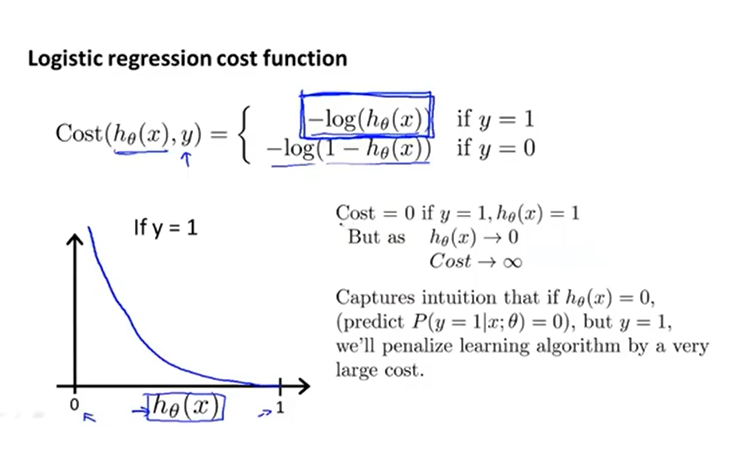
表示给定后的概率
假设预测的概率,而的真实值是,那选用第一个代价函数,此时为;如果的真实值是,那选用第二个代价函数,此时为。
将合并简化:
# 多元分类
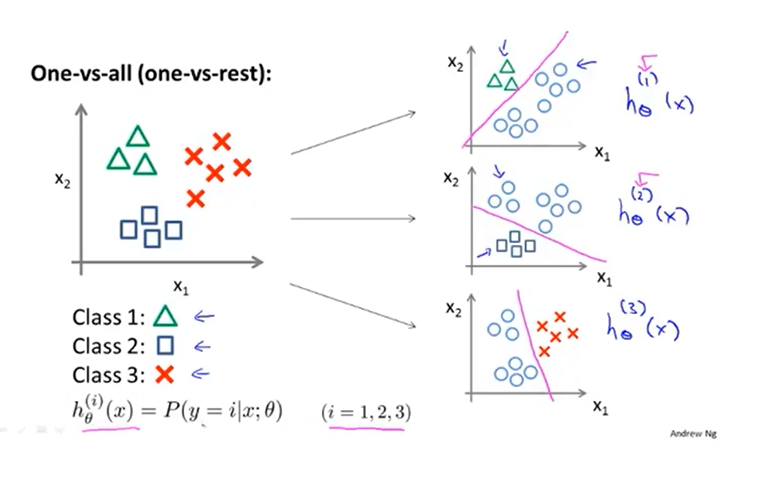
对于每个,将其转化为二分类问题,用上述回归的代价函数,结合梯度下降,训练各自的分类器,用来预测时的概率
对于一个新的输入,找到最大的即可,此时的便是预测的类。
INFO
不同的有不同的参数
# 正则化代价函数
正则化线性回归的代价函数:
INFO
训练集样本容量
参数个数
正则化项是为了使参数尽量地小,保证假设模型相对简单,避免过拟合
正则化逻辑回归的代价函数和上述类似,加一个正则化项。
# 神经网络
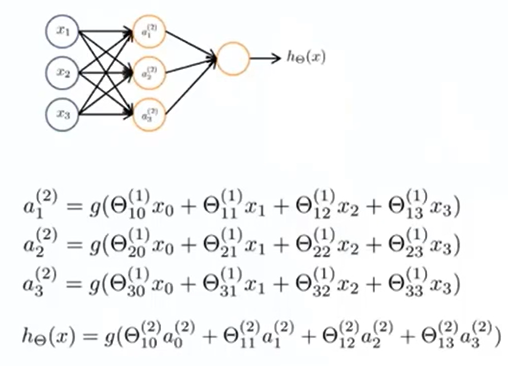
右上角的表示神经网络第层与第层之间的参数(或者说权重),右下角的表示的和的。
# 多元分类

图中是一个四分类问题,训练集,其中表示图片的特征,是一个四维的标签,我们想要让。
# 代价函数

和逻辑回归的代价函数类似,逻辑回归的代价函数(经过正则化)是
神经网络的代价函数是
INFO
神经网络层数
第层的神经元个数(不包括偏置单元)
代表输出层的单元数,等价于
是一个维向量,表示输出向量的第个值
# 反向传播

一开始让,用来计算
遍历训练集的每个样本
首先让输入层的激活函数
运用正向传播算法
计算之后每层的激活函数
然后用样本的标签(或者说真值),计算输出值的误差项
运用反向传播算法
计算,注意没有,因为不需要对输入层考虑误差项
最后让,或者写成向量形式
由此计算出
而我们所需要的偏导
得到了神经网络的代价函数关于每个参数的偏导项后,就可以使用梯度下降或者其他高级优化算法了。
INFO
表示点乘,为矩阵的对应位置相乘
# 梯度检测
反向传播算法可能会出现错误,因此需要用梯度检测来检验偏导,看是否近似
INFO
由于计算量非常大,因此在训练分类器之前,需要关掉梯度检测
# 随机初始化
如果将所有参数都初始化为0,会造成所有单元都相等的现象。为了避免这种情况,需要对参数进行随机初始化
# 训练集、验证集、测试集
先使用测试集对不同的假设模型得到参数
再用验证集选择出交叉验证误差最小的模型
然后用测试集计算泛化误差
# 偏差和方差
# 模型多项式次数与偏差、方差

如果训练集误差高,验证集误差也高(图中左侧红框),则是一个偏差问题;
如果训练集误差低,但验证集误差高(图中右侧红框),则是一个方差问题。
# 正则化参数与偏差、方差
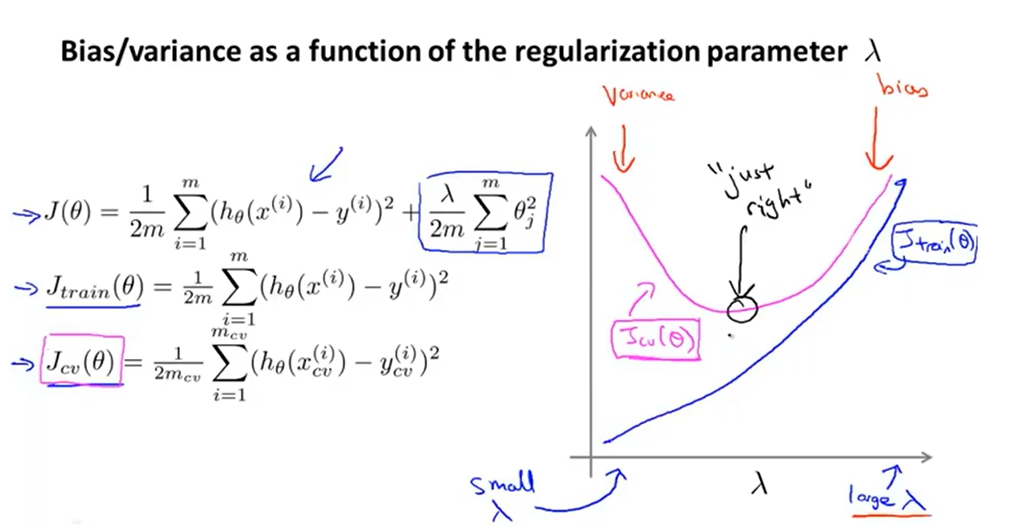
INFO
图中,包括正则化项,而不包括
通过取不同的值,让最小
得到对应的参数,计算在参数下的变化
越小,惩罚程度越小,正则化项可以忽略,可能会出现过拟合现象(正则化是为了防止过拟合现象),即对训练集的拟合效果非常好,此时很小;越大,惩罚程度越大,可能连训练集都不能很好地拟合,此时很大。
同理,在很小时,可能会出现过拟合现象,对应高方差问题,因此较大;在很大时,可能会出现欠拟合现象,对应高偏差问题,因此也较大。而中间总会有某个值,此时的表现刚好合适。
INFO
过拟合对应高方差问题,较小,但较大;
欠拟合对应高偏差问题,和都较大。
上述图像比较简单和理想化,真实数据可能更加凌乱且有很多噪声,但趋势总归是正确的
# 精确度和召回率

预测为1的数据中实际为1的比例
实际为1的数据中真正被预测为1的比例
# 精确度和召回率的权衡

通过改变,精确度和召回率会变化。具体来说,当增大时,会有更高的精确度(预测为1的数据中实际为1的比例更大)和更低的召回率(实际为1的数据不变,但由于更加保守,预测为1的数据变少了);当减小时,会有更低的精确度和更高的召回率。
两者不可兼得,可以使用来评估算法(当然,也有很多其他评估方式)
# 支持向量机
# 代价函数
支持向量机的代价函数和逻辑回归的代价函数类似
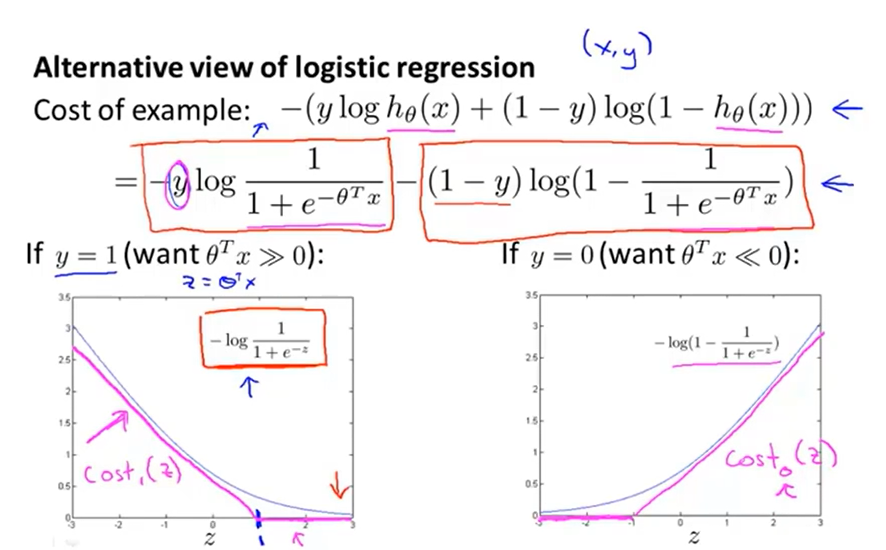

其中,和类似,前者是分段直线,后者是曲线(参考上图)
同时,去掉了参数,并从原来的形式变为了形式
当时,我们希望不仅仅是,而是,这样为,项就为,使代价函数尽量小,反之时希望。
当得到了使代价函数最小的参数后,带入交叉验证集/测试集的数据,就能得到支持向量机的输出
# 非线性决策边界
以高斯核函数为例,给定一个输入,得到
其中,是标记点,等同于训练样本点();可以是训练集,交叉验证集,测试集等等。
如果 如果距离很远,则,可以理解为相似度。

如图所示,靠近的点将会预测为,远离则为。
# 核函数与
对于训练样本,可以得到个,即
为训练样本的大小,因为标记点就是训练样本点,所以标记点有个,为维向量。

将映射为(描述第个训练样本的特征向量由变成),则变为。
INFO
和中的(维)和(维)的维度不一定相等,对应的维度也不一样。其中,是特征的维度,是训练样本大小
同样,正则化项中的等于的维度,由于图中的为维向量,则也为维向量,正则化项中的其实就等于
# 主成分分析

假如要将维降成维,则找出使得投影误差最小的向量,即点到投影后的点之间的距离。
要将维降成维,则找出使得投影误差最小的个向量。
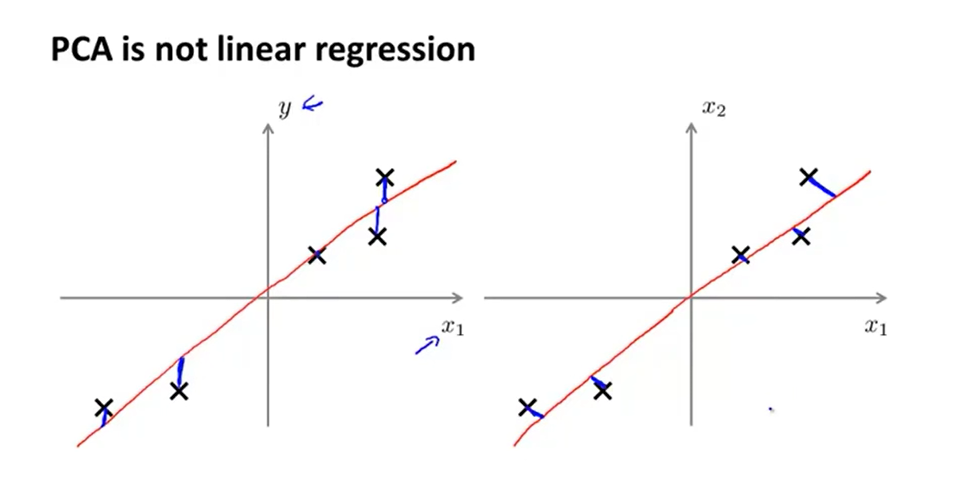
同时,主成分分析与线性回归不同,如上图所示,左边是线性回归,右边是,蓝色线段代表各自的误差,两者的误差并不相同。
# 主成分分析算法
将数据从维降到维
- 首先计算协方差矩阵
- 然后计算的特征向量矩阵
- 取前个向量组成
- 对于一个样本,降维后新的坐标
# 异常检测
# 原始模型

训练集为,样本有个特征
每一种特征都满足正态分布,计算参数
特征的平均值
特征的方差
然后对于一个新的特征向量,计算概率
如果概率,则是不正常的样本
INFO
参数为的正态分布在位置的概率
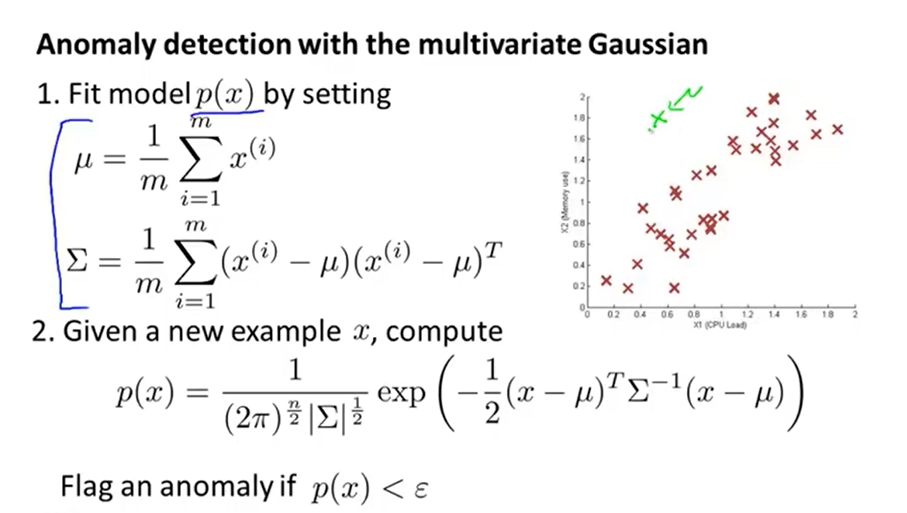
# 多元高斯模型
不再将多个特征视作独立分开的高斯分布,而是将看作一个多元高斯分布,参数,协方差矩阵
# 协同过滤算法
以电影评分为例,电影的特征为,能够描述电影的特点;用户的参数为。表示用户对电影的预测评分。

给出,能通过代价函数预测;反之,给出,能通过代价函数预测。
其中,表示用户评价了电影,表示用户对电影的实际评分。
协同过滤算法能同时最小化参数和,其代价函数为上图中前两个代价函数的组合。
首先将参数初始化为较小的随机值(和神经网络类似),通过梯度下降等方法将代价函数最小化,可以得到参数和。如果用户尚未评价电影,可以通过计算出预测的评分。
# 梯度下降
# 批量梯度下降
# 随机梯度下降
在批量梯度下降算法中,每次进行迭代都需要遍历所有的训练样本,并且整个流程会进行多次上述运算。在数据很多的时候计算量会非常大,需要运用到随机梯度下降。
随机梯度下降先打乱训练样本,然后依次遍历训练样本,进行迭代
这样,每遍历一个样本便进行了一次迭代,不需要频繁地遍历所有训练样本。

在上图中,红色是批量梯度下降的收敛过程,紫色是随机梯度下降的收敛过程。随机梯度下降的内层循环取决于训练集的大小,外层循环通常只需要进行1-10次。
# 梯度下降

批量梯度下降一次性用所有训练样本进行迭代;
随机梯度下降一次只用一个训练样本进行迭代;
而梯度下降则一次用个训练样本来迭代。